Research
Flat Hamiltonians are Topologically Trivial
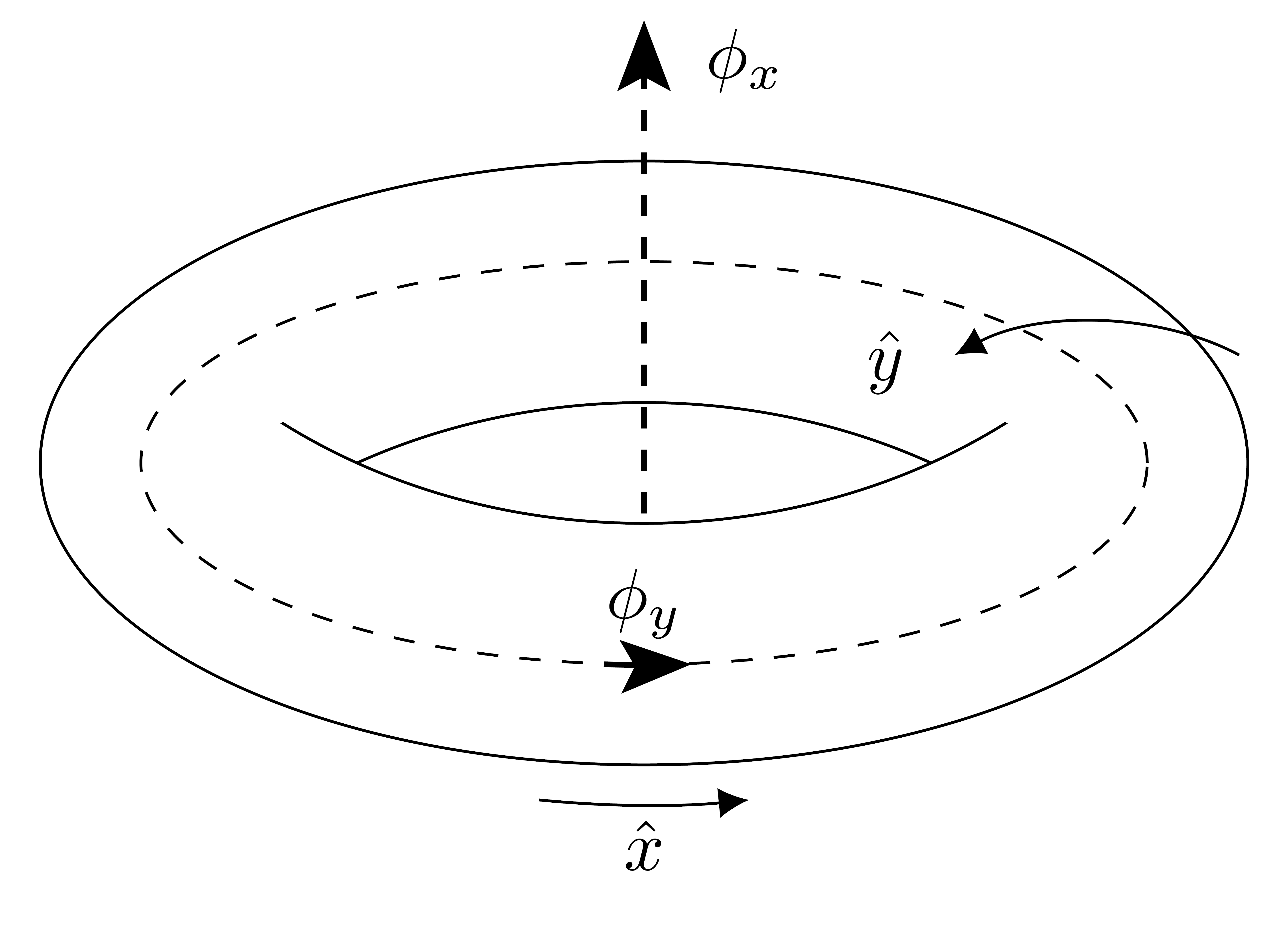
Landau levels play a key role in theoretical models of the quantum Hall effect. Each Landau level is degenerate, flat and topologically non-trivial. Motivated by Landau levels, we study tight-binding Hamiltonians whose energy levels are all flat. We demonstrate that in two dimensions, for such Hamiltonians, the flat bands must be topologically trivial. To that end, we show that the projector onto each flat band is necessarily strictly local. Our conclusions do not need the assumption of lattice translational invariance.
Publications:
Publications:
Compactly Supported Wannier Functions

Wannier functions have widespread utility in condensed matter physics and beyond. Topological physics on the other hand has largely involved the related notion of compactly supported Wannier-type functions which arise naturally in flat bands. In this work, we establish a connection between these two notions, by finding the necessary and sufficient conditions under which compact Wannier functions exist in one dimension. We present an exhaustive construction of models with compact Wannier functions and show that the Wannier functions are unique and in general, distinct from the corresponding maximally localized Wannier functions.
Publications:
Publications:
- Pratik Sathe and Rahul Roy. “Compact Wannier Functions in One Dimension.” arXiv: 2302.11608(2023). [link][PDF]
- Sathe, Pratik, Fenner Harper, and Rahul Roy. “Compactly supported Wannier functions and strictly local projectors.” Journal of Physics A: Mathematical and Theoretical 54.33 (2021): 335302. [link][PDF]
Scattering Expansion for Localization in One Dimension

We present a perturbative approach to a broad class of disordered systems in one spatial dimension. Considering a long chain of identically disordered scatterers, we expand in the reflection strength of any individual scatterer. This expansion accesses the full range of phase disorder from weak to strong. As an example application, we show analytically that in a discrete-time quantum walk, the localization length can depend non-monotonically on the strength of phase disorder (whereas expanding in weak disorder yields monotonic decrease). Returning to the general case, we obtain to all orders in the expansion a particular non-separable form for the joint probability distribution of the log-transmission and reflection phase. Furthermore, we show that for weak local reflection strength, a version of the scaling theory of localization holds: the joint distribution is determined by just three parameters.
Publications:
Publications:
Universal Delocalization Transition in Chiral Floquet Topological Insulators

Periodically driven (Floquet) systems often exhibit behavior distinct from undriven systems. Any amount of disorder in one-dimensional undriven systems generically localizes all eigenstates. In contrast, we show that in topologically non-trivial, non-interacting Floquet loop drives with chiral symmetry, a delocalization transition occurs at as the time \(t\) is varied within the driving period (\(0< t< T_{drive}\)). We find that the localization length L loc at all quasienergies diverges with a universal exponent of \(2\) as \(t\) approaches the midpoint of the drive: \(L_{loc}~(t-T_{drive}/2)-2\). We provide numerical evidence for the universality of this exponent by studying a variety of such drives using exact diagonalization, and we also present an analytical argument based on scattering theory.
Benchmarking of Iterative Quantum Classical Algorithms

The benchmarking of quantum computers is crucial to understand the capabilities of existing quantum computing hardware, which in turn enables us to figure out how to improve them. One approach is to implement applications on quantum hardware and assess the performance by devising appropriate metrics, and capturing them during the implementation. Combinatorial optimization is anticipated to be one of the primary use cases for quantum computation in the coming years. Quantum Approximate Optimization Algorithm (QAOA) and Quantum Annealing (QA) are expected to demonstrate significant run-time performance benefits over classical solutions. By using existing methods for characterizing the performance of classical optimization algorithms, we compare solution quality obtained by solving Max-Cut problems using a quantum annealing device and gate-model quantum simulators and devices. This is used to guide the development of an advanced benchmarking framework for quantum computers designed to evaluate the trade-off between run-time execution performance and the quality of solution for iterative hybrid quantum-classical applications. Of particular relevance is how the nature of the problem input configuration impacts the solution quality, the length of time required to achieve a solution, and the algorithm limitations uncovered by the benchmarking approach. The framework is an enhancement to the existing open-source QED-C Application-Oriented Benchmark suite. The suite can be executed on various quantum simulators, quantum hardware backends, and a quantum annealing device.
GitHub repository link.
GitHub repository link.
Search and Rescue at Sea Aided by Hidden Flow Structures

Every year, hundreds of people die at sea because of vessel and airplane accidents. A key challenge in reducing the number of these fatalities is to make Search and Rescue (SAR) algorithms more efficient. Here, we address this challenge by uncovering hidden TRansient Attracting Profiles (TRAPs) in ocean-surface velocity data. Computable from a single velocity-field snapshot, TRAPs act as short-term attractors for all floating objects. In three different ocean field experiments, we show that TRAPs computed from measured as well as modeled velocities attract deployed drifters and manikins emulating people fallen in the water. TRAPs, which remain hidden to prior flow diagnostics, thus provide critical information for hazard responses, such as SAR and oil spill containment, and hence have the potential to save lives and limit environmental disasters.
Publications:
Publications:
Uncovering the Edge of the Polar Vortex

The polar vortices play a crucial role in the formation of the ozone hole and can cause severe weather anomalies. Their boundaries, known as the vortex ‘edges’, are typically identi- fied via methods that are either frame-dependent or return non-material structures, and hence are unsuitable for assessing material transport barriers. Using two-dimensional velocity data on isentropic surfaces in the northern hemisphere, we show that elliptic Lagrangian Coherent Structures (LCSs) identify the correct outermost material surface dividing the coherent vortex core from the surrounding incoherent surf zone. Despite the purely kinematic construction of LCSs, we find a remarkable contrast in temperature and ozone concentration across the identified vortex boundary. We also show that potential vorticity-based methods, despite their simplicity, misidentify the correct extent of the vortex edge.
Publications:
Publications: